Calibration Transfer, Part V: The Mathematics of Wavelength Standards Used for Spectroscopy

How does one compute the mathematical certainty of wavelength standards used for calibrating instrumentation used for molecular spectroscopy measurements? This question becomes of major importance when the technique used for measurement requires the collection of large databases for use in qualitative searches or quantitative multivariate analysis. Wavelength drift over time within a single instrument or wavelength differences between instruments create errors and variation in the accuracy of measurements using databases collected with different wavelength registrations. The loss of integrity over the wavelength axis of data collected over time is a significant problem in large database creation and usage. So, what are the techniques and mathematics used to compute uncertainty, and the optimum methods for maintaining wavelength accuracy within instrumentation over time, when considering measurement condition changes?

Wavelength precision and accuracy, more formally termed repeatability and reproducibility, within a single instrument and between multiple instruments over time are essential for optimum transfer of quantitative calibrations, and for the continuous use of databases in qualitative search techniques. To maintain the integrity of data, it is essential that the wavelength axis be stable within instruments and identical across different instruments over changing measurement conditions. This is a difficult task for the basic commercial instrument designers and manufacturers in terms of making spectrometers highly precise and accurate on the wavelength axis. Questions arise as to the engineering tolerances required for high-precision spectrometers in terms of mechanical, optical, and electronic components. Also essential to the precise wavelength alignment are the exact procedures required to properly calibrate the wavelength axis of the spectrometer based on measurements of known reference standards (1,2).

Different Approaches to Alignment of the Wavelength Axis

Because of the inherent uncertainties of standard reference materials (SRMs), one may ask if they are precise enough to be useful for aligning the wavelength axis of spectrometers over time (3). For example, National Institute of Standards and Technology (NIST) SRM 1920a reported a published uncertainty of ±1 nm (4,5). With large uncertainties in published wavelength peak positions, referred to as measurands, is the most reasonable approach to ensure that wavelength accuracy is within inherent NIST uncertainties when using SRMs, but strive to be far closer in agreement for instrument-to-instrument matching? This column demonstrates the state of the art in commercial spectrometers today and proposes the question of whether there might be improved methods for spectrometer wavelength alignment for enhanced repeatability and reproducibility.

A seminal paper on the use of rare-earth oxides for use as wavelength standards in near infrared (NIR) spectroscopy is familiar to many spectroscopists (4). One important wavelength standard made for use in the NIR region is SRM 1920a, consisting of a mixture of rare-earth oxides. This SRM has known stability problems related to variation in wavelength scale and, as such, has been replaced with SRM 2036 glass (6). SRM 1920a is not a particularly stable material and wavelength registration changes based on temperature have been published as (±0.15 nm). In the certification of SRM 1920a, NIST also experienced challenges with their secondary Cary model spectrometer and their manual method of peak selection resulting in the large reported uncertainty (4). In calibrating this SRM, NIST reportedly used the precise NIST (formerly the National Bureau of Standards [NBS]) spectrometer to measure three wavelengths (that is, 1012.9, 1260.7, and 1535.5 nm). The Cary instrument was reported to exhibit a deviation of ±1 nm during the test measurement period. For the NIST spectrometer, emission reference lamps included the use of neon (Ne) at 703.24 nm, xenon (Xe) at 881.94 and 979.97 nm, mercury (Hg) at 1013.97 and 1529.58 nm, and krypton (Kr) at 1816.73 nm. The use of such atomic line spectra for wavelength registration produces the lowest uncertainty (7).

For the longer NIR wavelength region, 1,2,4-trichlorobenzene was used to mark the 2152.60 nm position (8). Toluene (used for infrared at 3290.8, 3422.0, 3484.0, 5147.2, 5381.8, and 5549.0 nm) and carbon disulfide (2224.0 nm) have also been recommended for wavelength calibration in early published work (9,10). The task of selecting appropriate standards for certified peak wavelength positions is critical for improved x-axis (wavelength) alignment and calibration of spectrometers. Wavelength alignment technology is dependent on selecting a suitable set of reference peak wavelengths and stable materials to align each spectrometer system using best available measurement practices. If wavelength precision must approach ±0.05 nm and accuracy across the entire spectral region must be better than ±0.2 nm for 95% confidence interval, a series of technological improvements must be implemented in the future.

So, what if a master instrument, with its own idiosyncratic scanning features, can be duplicated? One might analyze a paired reference standard with the master instrument and align the newly manufactured instrument to the set of wavelength peak position values found using the master instrument. This approach was used in the early development of NIR instruments in an attempt to make them more similar (11–13). The problem with this approach is the entire world may have a different set of nominal wavelength values (measurands) than the master instrument. Spectrometers change over time and conditions and wavelength alignment drifts. A common spectrometer may demonstrate inherent nonlinearity in its wavelength axis, which does not allow accurate alignment throughout the complete spectral range. So to consistently align the wavelength axis with other instrument types, and even to align a single instrument over time, requires not only repeatability, but also accuracy indicated by agreement with reference standard peak positions (measurands). These reference peak positions are provided by a set of known physical standards (physical in the sense of primary lines that are universally reproducible). Such standards may be primary emission standards (that is, atomic lines), physical standards of mixed rare earth glasses, or even organic liquids at standard pathlength and temperature. The measurands for calibrating wavelength scales would optimally be obtained using first principles whenever possible because this approach is universal and based on sound physical science and metrology, which by definition is fixed to a specific known uncertainty. The national laboratories around the globe use this approach as much as possible (14,15). There are other materials that may be used as physical standards, such as etalons. The use of etalons for wavelength alignment was successfully implemented for a process diode array spectrometer (16–20). The instrument was extremely precise, but too expensive for market acceptance because the spectrograph had originally been designed for the harsh conditions of an Earth-orbiting satellite.

To determine a unique set of peak wavelength values based on an arbitrary master instrument does not serve our purposes adequately over time. One would ideally expect high precision with universal accuracy so that databases now and in the future may be aligned with any instrument technology and be carried reproducibly into the future. In addition, using a first principles approach allows one to standardize the data based on known wavelength positioning at any time. By using first principles, wavelength alignment may be defined electronically and, thus, no physical instrument or object is required to transfer the technology required for wavelength axis calibration. What is required to make all this work are repeatable and well-characterized peak wavelength standards, either emission sources, pure compounds, or solid rare-earth oxide glasses with known peak wavelength positions, stability, and well-defined uncertainty. Requirements are for glasses, crystalline polymers, and pure chemical solutions with an uncertainty of better than ±0.1 nm for multiple wavelengths. For infrared and Raman systems the uncertainty should be better than ±0.1% and better than 0.05 cm^-1 (wavenumber) (21). If a spectrometer is repeatable, but not reproducible (accurate), then database and calibration transfer becomes an issue of trying to align the wavelength axis to some unknown or poorly defined system.

The NIST Uncertainty Number for SRMs

NIST uncertainty is a true measure of uncertainty, unlike the typical manufacturer report as either precision or accuracy. For example, NIST uncertainty has been calculated from equation 1 (4):

where A = twice the largest standard deviation of measurement of multiple emission lines (measurands) versus the spectrometer measured values over a period of 31 days (or some designated period); B = twice the standard deviation of the uncertainty in the peak selection method used; and C is the maximum variation in the standard because of temperature changes over a specified range and conditions. (Note: The number 2 (twice) is referred to as the k value also known as the coverage factor; see reference 14).

In testing SRM 1920a, the reported error for multiple wavelengths using emission lines for the NIST spectrometer was ±0.265 nm for all the data points measured over 31 days. The NIST actual reported uncertainty for SRM 1920a is equal to equation 2.

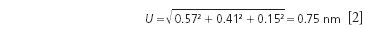
This value was rounded up to ±1 nm considering the added uncertainty of the Cary spectrometer measurements and material stability over the lifetime of the SRM (4).

A more detailed description of uncertainty computations and rationale with respect to wavelength SRMs is found in other published work (6,14,22). There are significant complexities to the question of uncertainty in reference materials, so the reader is referred directly to the three citations referenced above. One may also obtain more detailed information on the history of the international metrical committees responsible for defining the technical details for uncertainty associated with measurement results; the reader is referred to appendices C and D in reference 14 for historical details.

Commercial Instrument Wavelength Data

Let us begin with a set of measurement data as shown in Table I. This is real data measured on a series of commercially calibrated NIR spectrometers using an identical sample to measure a variety of performance characteristics. For this column, we refer to the wavelength measurement data across the A–G instruments consisting of seven commercial instrument models manufactured by four companies. These will remain anonymous for the purpose of this analysis. Please note that within the models used for this experiment, there were dispersive monochromators, diode-array based instruments, and Fourier transform near-infrared (FT-NIR) systems.

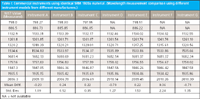
Table I: Commercial instruments using identical SRM 1920a material. (Wavelength measurement comparison using different instrument models from different manufacturers.)

This table demonstrates the instrument models A through G as individual columns, with the different nominal wavelength values (measurands) for the SRM 1920a standard material along the first column. The results of a set of standard spectra are shown in each column demonstrating the peak positions as determined using a five-point cubic spline, peak interpolation method. No data processing or smoothing was applied to the spectra, but after the manufacturers' recommended calibration the reference material was measured using three replicates. For Tables I and II a single spectrum was selected for identification of peak position. For Table III each of the replicate spectra are used for computing the reported parameters. The reported wavelengths are shown as compared to the NIST nominal wavelengths (measurands) for a nominal bandwidth of 10 nm. The last two rows show the mean difference and standard deviation between the measured values and the measurand values for each peak, respectively, for the complete set of instrument measurements at each wavelength. One may quickly observe that relatively large differences between the measurand and measured wavelengths are present in the commercial world of NIR spectrometers.

Table II: Results of commercial instruments on SRM 1920a for each nominal wavelength (measurand 10 nm bandwidth values as top row)

From Table I it may be observed that there is significant variation from commercial NIR instruments and published nominal wavelength positions for this reference standard. Let's review these results from a measure of uncertainty viewpoint.

Table III: Wavelength precision and accuracy across different manufacturers using a 1-mm-thick crystalline polystyrene standard (nominal 10 nm bandwidth)

For wavelength accuracy (standard deviation of error between the measured and measurand values), we may compute the standard deviation of difference for each measured wavelength collected across n instruments, for the measured (λ_ij) versus measurand or reference (λ_ref) wavelength values. Therefore, the standard deviation at each wavelength is calculated as equation 3:

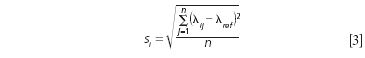
The mean difference between the measured and measurand values for wavelength "accuracy" is determined by equation 4:

Where λ(withbar)_i is the average peak wavelength for the instrument measurements for each peak wavelength; and λ_ref is the reference (measurand) wavelength position for the standard at each peak wavelength. The results are reported as: wavelength (nm) "precision" (repeatability) and standard deviation of error "accuracy" as shown. This may be accomplished for multiple wavelengths depending on the standard reference material measured.

The Relative Standard Uncertainty Across Commercial Instruments

Let's look at this as a pooled standard deviation of error for all measured wavelengths for all instruments. The pooled standard deviation of error between all measured wavelength values as compared to the NIST measurand values across all commercial instruments for the identical standard sample is calculated using the pooled standard deviations from Table II and is computed to be 1.303 nm.

Then the confidence levels for a randomly selected commercial spectrometer would be expressed as follows:

For 68%, y_i ± u(y_i) = nominal (measurand) NIST wavelength for SRM ±1.303 nm

For 95%, y_i ± 2 · u(y_i) = nominal (measurand) NIST wavelength for SRM ± 2.606 nm

So, the expression of uncertainty for this example of data would be

y = nominal (measurand) NIST wavelength for SRM ±1.303 nm or

y = nominal (measurand) NIST wavelength for SRM (1.303)U

The results in Table I indicate that for many multivariate equations where precise wavelength alignment (or agreement) is critical for accurate calibration transfer, with minimal bias and slope changes, one can envision a large technical difficulty in transferring multivariate calibration models from one current instrument type to another and one instrument manufacturer to another.

Note that we use the above equation for wavelength standard deviation of error between the measured values and the measurand values "accuracy" and the following equation for wavelength repeatability. For instrument wavelength repeatability, repeat measurements of the same standard were made by placing it in the sample beam and not mechanically moving the sample over a normal measurement cycle for the instrument. For example, a 30 s measurement period and 15 s reference spectrum may be typical. Then the peak position was determined for each replicate measurement and reported. Then using the mean spectrum wavelength position (λ(withbar)_i) for the measured wavelength value (λ_ij), the repeatability is computed as equation 5.

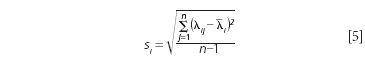
Where s_i is the standard deviation for the scan-to-scan wavelength (as precision or repeatability) for the instrument under the specific measurement conditions; λ_ij are individual wavelength peak positions for sample i and scan number j; λ(withbar)_i is the average peak position value for the replicate scan set; and n is the number of replicate measurements.

The mean spectrum wavelength position (λ(withbar)_i) is calculated as equation 6.

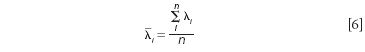
From the data in Table I we may compute the following tabular results (as shown in Table II).

Now, if one looks at repeatability and the standard deviation of error between the measured values and the measurand values within a single instrument based on crystalline polystyrene, the following data (Table III) are found.

The Confidence Levels and Uncertainty Across Commercial Instrument Manufacturers A through D

Now let's look at this as a pooled standard deviation of error for both measured polystyrene wavelengths combined. The overall standard deviation for both measured wavelengths across the four manufacturers commercial instruments for the same standard sample is calculated using the pooled standard deviations for the replicate measurements. The following confidence levels are the result.

Instrument Manufacturer A

The confidence levels would be expressed as follows:

For 68%, yi ± u(yi) = nominal (measurand) wavelength for standard ±0.312 nm

For 95%, yi ± 2 · u(y_i) = nominal (measurand) wavelength for standard ± 0.624 nm

So, the expression of uncertainty for this example of data would be

y = nominal (measurand) wavelength for standard ± 0.312 nm or

y = nominal (measurand) wavelength for standard (0.312)U

Instrument Manufacturer B

The confidence levels would be expressed as follows:

For 68%, y_i ± u(y_i) = nominal (measurand) wavelength for standard ±1.205 nm

For 95%, y_i ± 2 · u(y_i) = nominal (measurand) wavelength for standard ±2.410 nm

So, the expression of uncertainty for this example of data would be

y = nominal (measurand) wavelength for standard ± 1.205 nm or

y = nominal (measurand) wavelength for standard (1.205)U

Instrument Manufacturer C

The confidence levels would be expressed as follows:

For 68%, yi ± u(yi) = nominal (measurand) wavelength for standard ±0.657 nm

For 95%, yi ± 2 · u(yi) = nominal (measurand) wavelength for standard ± 1.314 nm

So, the expression of uncertainty for this example of data would be

y = nominal (measurand) wavelength for standard ± 0.657 nm or

y = nominal (measurand) wavelength for standard (0.657)U

Instrument Manufacturer D

The confidence levels would be expressed as follows:

For 68%, yi ± u(yi) = nominal (measurand) wavelength for standard ± 0.821 nm

For 95%, yi ± 2 · u(yi) = nominal (measurand) wavelength for standard ± 1.642 nm

So, the expression of uncertainty for this example of data would be

y = nominal (measurand) wavelength for standard ±0.821 nm or

y = nominal (measurand) wavelength for standard (0.821)U

Using a NIST-Like Uncertainty Measurement

You will see from the data shown in the Tables I and II (with a pooled standard deviation of ±1.303 nm) that for a typical commercial instrument one may estimate the uncertainty with respect to wavelength accuracy (or agreement between measured wavelength peaks and measurand peak locations). Therefore, using the same uncertainty formula as NIST, a commercial instrument measured uncertainty for SRM 1920a is closer to the results shown in equation 7.

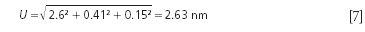
Conclusion

So, one must be careful when using the term uncertainty; NIST uncertainty is very well defined and does not relate to a simple measurement and standard deviation computation. Although results within the instrument wavelength repeatability or precision might be considered reasonable for commercial NIR spectrometers from Table II, the uncertainty of the wavelength registration as measured using solid reference materials and comparing those results to measurand values is far from perfection. In some future columns we plan to address additional methods and computations for wavelength and wavenumber axis alignment of various spectrometers using first principles.

References

(1) Y. Wang, D.J. Veltkamp, and B. Kowalski, Anal. Chem. 63, 2750–2756 (1991).

(2) J. Workman, Jr., and H. Mark, Spectroscopy 28(10), 24–33 (2013).

(3) C. Burgess and J. Hammond, Spectroscopy 22(4), 40–48 (2007).

(4) V.R. Weidner, P.Y. Barnes, and K.L. Eckerle, J. Research NBS 91(5), 243–253 (1986).

(5) "Standard Reference Material (SRM) 1920a Certificate of Analysis, Near-Infrared Reflectance Wavelength Standard from 740 nm to 2000 nm," (National Institute of Standards and Technology [NIST], Gaithersburg, Maryland, 20899, 7 pages, 2 February, 2006).

(6) "Standard Reference Material (SRM) 2036 Certificate, Near-Infrared Wavelength/Wavenumber Reflection Standard," (National Institute of Standards and Technology [NIST], Gaithersburg, Maryland, 20899, 7 pages, 24 January 2013).

(7) "Basic Atomic Spectroscopic Data" (National Institute of Standards and Technology [NIST], Gaithersburg, Maryland, 20899). Available at: http://physics.nist.gov/PhysRefData/Handbook/element_name.htm.

(8) K.W. Busch, O. Soyemi, D. Rabbe, K. Humphrey, B. Dundee, and M.A. Busch, Appl. Spectrosc. 54(9), 1321–1326 (2000).

(9) N. Acquista and E.K. Plyler, J. Research NBS 49(1), 13–16 (1952).

(10) E.K. Plyler, L.R. Blaine, and M. Nowak, J. Research NBS 58(4), 195–200 (1957).

(11) J.S. Shenk, M.O. Westerhaus, and W.C. Templeton, Crop Sci. 25, 159–161 (1985).

(12) K.G. Nordqvist, U.S. patent 4,944,589 (1990).

(13) J.S. Shenk and M.O. Westerhaus, Crop Sci. 31, 1694–1696(1991).

(14) B.N. Taylor and C.E. Kuyatt, Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, (National Institute of Standards and Technology [NIST], Gaithersburg, Maryland, Technical Note 1297, 20 pages, 1994).

(15) A. Springsteen, Spectroscopy Global Edition, 6-9, November (2006).

(16) J. Coates, T. Davidson, and L. McDermott, Spectroscopy 7(9), 40–49 (1992).

(17) J. Workman, Jr., and John Coates, Spectroscopy 8(9), 36–42 (1993).

(18) D. Tracy, R. Hoult, and A. Ganz, U.S. patent 5,303,165 (1994).

(19) J. Workman, "Diode Array Process Instrumentation in the Near Infrared," in Proc. 2nd Oxford Conference on Spectroscopy, (Franklin Pierce College, Rindge, New Hampshire, June 1994).

(20) J. Workman, L. McDermott, B. DeSimas, and J. Coates, JPAC 2, 444–450 (1996).

(21) L.M. Hanssen and C. Zhu, in Handbook of Vibrational Spectroscopy, J. Chalmers and P.R. Griffiths, Eds. (John Wiley & Sons Ltd., Chichester, England, 2002).

(22) S.J. Choquette, D.L. Duewer, L.M. Hanssen, and E.A. Early, Appl. Spectrosc. 59(4), 496–504 (2005).

Jerome Workman, Jr. serves on the Editorial Advisory Board of Spectroscopy and is the Executive Vice President of Engineering at Unity Scientific, LLC, (Brookfield, Connecticut). He is also an adjunct professor at U.S. National University (La Jolla, California), and Liberty University (Lynchburg, Virginia). His e-mail address is JWorkman04@gsb.columbia.edu

Jerome Workman, Jr.

Howard Mark serves on the Editorial Advisory Board of Spectroscopy and runs a consulting service, Mark Electronics (Suffern, New York). He can be reached via e-mail: hlmark@nearinfrared.com

Howard Mark