Effect of Dopants or Impurities on the Raman Spectrum of the Host Crystal

The disruption of crystalline symmetry by dopants or impurities in a crystal can affect the lattice vibrational modes of the host crystal. The manner in which the host-crystal Raman spectrum is affected is related to the site occupancy of the dopant or impurity. Not all bands are affected equally by the presence of heterogeneity in the crystal. Those Raman bands arising from lattice vibrational modes that involve a significant contribution of atomic motion from the substituted atom will manifest the most significant broadening or shifting of peak position. The purpose of this installment of "Molecular Spectroscopy Workbench" is to inform and educate users of Raman instrumentation about the effect of dopants or impurities on the Raman spectra of crystals. We do that here through a detailed discussion of the effects of dopants on the Raman spectra of ZrGeO₄ in the scheelite phase.

Readers of "Molecular Spectroscopy Workbench" are aware that Raman spectroscopy is a convenient method for probing the chemical bonding and solid state structure of crystals. Moreover, it is sensitive to the presence of dopants, impurities, and crystal defects in the host-crystal lattice. The disruption of crystalline symmetry by dopants or impurities in a crystal can affect the lattice vibrational modes of the host crystal. If present at low concentrations (<1%), then the effect on the host lattice vibrational modes may not be perceptible. However, at levels greater than 1% dopants or impurities can be detected through the shifting and broadening of Raman bands of the host crystal. Moreover, new bands may appear that are absent in the Raman spectrum of the undoped or pure crystal. The manner in which the host-crystal Raman spectrum is affected is related to the site occupancy of the dopant or impurity. Therefore, one can infer from changes in the spectrum that dopants or impurities are present. Furthermore, the location of the dopants or impurities in the crystal lattice can be inferred from the particular bands affected. The purpose of this installment is to inform and educate users of Raman instrumentation about the effect of dopants or impurities on the Raman spectra of crystals. We do that here through a detailed discussion of the effects of dopants on the Raman spectra of ZrGeO₄.

ZrGeO₄ in the scheelite phase belongs to the C_4h crystal point group. Chains of 8-coordinate Zr⁴⁺ cations populate the ab-plane in the directions of the respective axes, whereas isolated GeO₄^4- tetrahedra alternate with the Zr⁴⁺ cations along the c-axis. A significant aspect of this structure is that the GeO₄^4- tetrahedra are distorted and exhibit compression along the c-axis. When activated by the presence of transition metal or lanthanide dopants, HfGeO₄ and ZrGeO₄ exhibit a broad blue luminescence when excited with X-rays. To understand the nature of the blue luminescence, studies have been performed to determine the local environment of the dopants (1). Specifically, there is a desire to know whether the dopant occupies the eightfold Zr⁴⁺ site or the fourfold GeO₄^4- tetrahedral coordination spheres.

The identification and assignment of those Raman bands most affected by the presence of transition metal or lanthanide dopants can be used to determine the site occupancy of the dopants. The first step is to assign the Raman bands to internal and external lattice vibrational modes. Here our distinction between internal and external modes pertains to the vibrational motions of the isolated GeO₄^4- tetrahedra. Those vibrational motions of the tetrahedra in which the center of mass does not move are regarded as internal modes. These modes approximate those of an isolated tetrahedron. In contrast, external modes are assigned to translational movement of the cation or tetrahedron or rotational motion of the tetrahedron as a whole. Regarding the rotational motions, external modes that involve the rotation of molecular groups about the center of mass are known as librational modes.

The irreducible representations of the optical phonons derived from a group theoretical treatment are

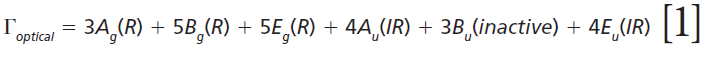
Click here to view full-size graphic

where IR, R, and inactive represent infrared-active, Raman-active, and inactive modes, respectively. Furthermore, site-group analysis predicts the following external translational and librational modes:

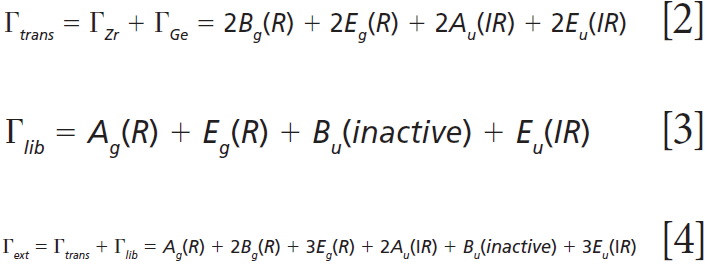
Click here to view full-size graphic

The remaining internal modes can be attributed to the vibrational motions of the GeO₄ group:

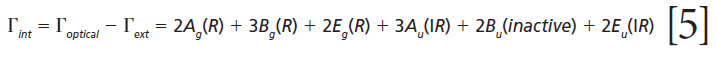
Click here to view full-size graphic

The polarizability tensors for the Raman active modes are

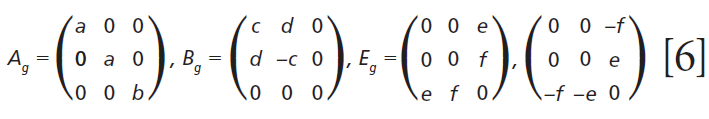
Click here to view full-size graphic

A Raman spectrum from a single crystal of ZrGeO₄ is shown in Figure 1. This spectrum was obtained from one face of a single crystal, so the relative intensities of the bands will not be the same as those from another face of this same crystal or from a spectrum obtained from a powder sample of ZrGeO₄. That is an important consideration when comparing this spectrum of ZrGeO₄ with those obtained from other ZrGeO₄ crystals doped with other elements. Differences in the relative intensities of Raman bands between spectra from doped and undoped crystals are only meaningful when comparing spectra acquired from the same crystallographic faces with the same crystal orientation and incident laser polarization. The bands in the Raman spectrum of ZrGeO₄ shown in Figure 1 have been assigned to external translational, librational, and internal modes based on previous work (1–3). Only 11 of the 13 Raman active modes expected based on equation 1 are labeled in Figure 1 because not all of the bands are sufficiently strong in this particular crystal orientation.

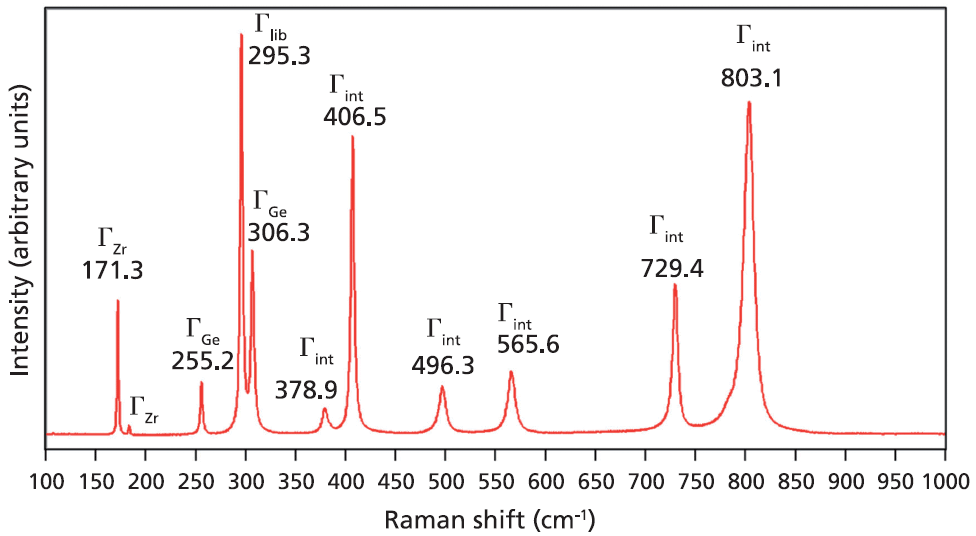
Figure 1: Raman spectrum obtained from a single crystal of ZrGeO₄.

Raman Spectroscopy of V- and Tb-Doped ZrGeO₄

Single crystals of ZrGeO₄ were prepared from a Li₂MoO₄•2MoO₃ flux containing 2 wt% ZrO₂ and fivefold excess of GeO₂. Dopants were added in the form of vanadium, terbium, or titanium oxides at various mole percentages (mol %) of the ZrO₂ value. Further details regarding crystal preparation can be found in a previous publication (1).

A Raman spectrum of vanadium-doped ZrGeO₄ along with that of undoped ZrGeO₄ for comparison are shown in Figure 2. The spectra were obtained from different crystallographic faces so differences in relative intensities of the spectra are expected. However, the differences in peak positions and band widths in the spectrum of the doped crystal can be attributed to disruption of the crystal lattice by the presence of V within the ZrGeO₄. We begin our analysis of the spectra by considering the bands that show little difference or a slight positive shift between the undoped and V-doped ZrGeO₄ at 171.8, 255.0, and 307.0 cm^-1 (ZrGeO₄:V⁴⁺ peak positions). These bands are assigned to external modes of Zr and Ge motion, and the shifts of the bands because of the presence of V are +0.5, -0.2, and +0.7 cm^-1, respectively. Conversely, the bands at higher energy all shift to lower wavenumbers and by more than 1 cm^-1 as a result of the presence of V. In particular, note the -6.5 cm^-1 shift from 295.3 cm^-1 in the spectrum of pure ZrGeO₄ to 288.8 cm^-1 in the V-doped spectrum. The directions and magnitudes of the changes in all band positions vary depending on the nature of the underlying lattice vibrational mode. In addition to the peak shifting, one can observe band broadening as a result of the doping. In particular, note how broad the 377.0 cm^-1 band is in the V-doped spectrum compared to its counterpart at 378.9 cm^-1 in the spectrum of ZrGeO₄. The 377.0 and 402.8 cm^-1 bands are only partially resolved in the V-doped spectrum whereas their counterparts in the spectrum of undoped ZrGeO₄ are completely resolved. The disruption of long-range translational symmetry by the dopant at a crystal lattice site causes an increase in the distribution of phonon energy states and therefore a broadening of the Raman bands. Not all bands are affected equally by the presence of heterogeneity in the crystal. Those Raman bands arising from lattice vibrational modes that involve a significant contribution of atomic motion from the substituted atom will manifest the most significant broadening.

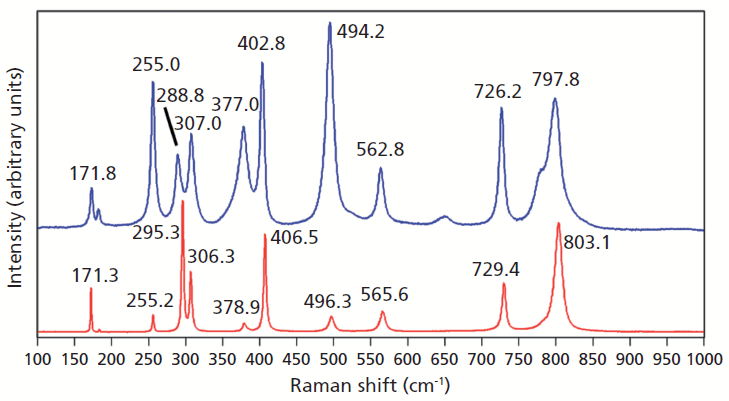
Figure 2: Raman spectra of single crystals of ZrGeO₄ (red) and ZrGeO₄ doped with V (blue).

Doping ZrGeO₄ with terbium produces changes in the Raman spectrum similar to, but not as great in magnitude, as those observed in the spectrum of V-doped ZrGeO₄. A Raman spectrum of terbium-doped ZrGeO₄ along with that of undoped ZrGeO₄ for comparison are shown in Figure 3. You can see from the similar relative intensities of the bands of the spectra of doped crystals in Figures 2 and 3 that the Raman spectra were acquired from the same crystallographic faces of the V- and Tb-doped crystals. In general, the bands shift and broaden with Tb doping just as observed for V doping. However, the changes in the spectrum of Tb-doped ZrGeO₄ are not as great as those observed for V-doped ZrGeO₄. In particular, the 378.5 cm^-1 peak in the Tb-doped ZrGeO₄ spectrum is not as broad as its counterpart at 377.0 cm^-1 in the V-doped ZrGeO₄ spectrum. The dopant levels are similar in these two crystals, so we might expect the effects on the ZrGeO₄ Raman spectrum to be similar as well. However, the effects of V doping are clearly greater than those from Tb. Why is that? To help us answer that question, we examine the effects of a third dopant, titanium, on the Raman spectrum of ZrGeO₄. Titanium is a transition metal immediately following vanadium in the periodic table of elements, whereas terbium is a lanthanide. We expect the chemical bonding of the transition metal dopants to the surrounding atoms to be different from that of the lanthanide.

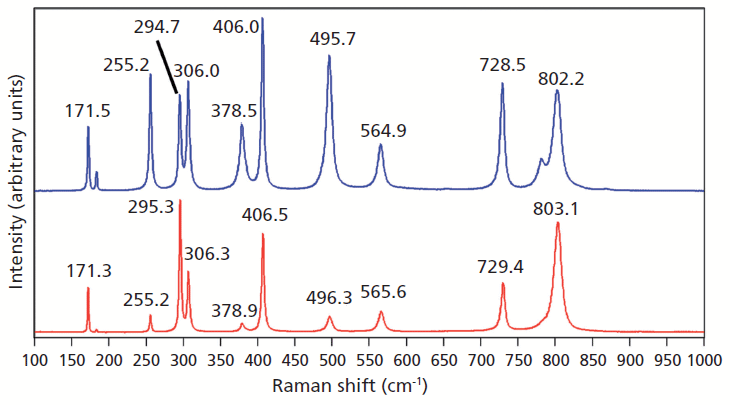
Figure 3: Raman spectra of single crystals of ZrGeO₄ (red) and ZrGeO₄ doped with Tb (blue).

Raman Spectroscopy of Titanium-Doped ZrGeO₄

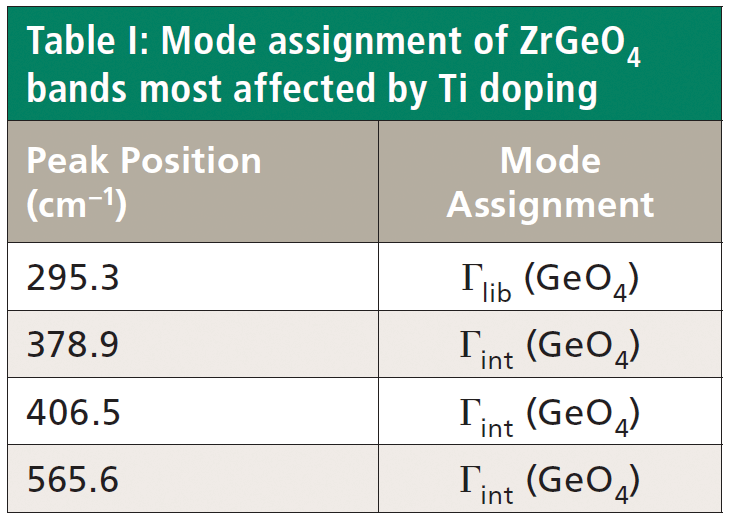
Crystals were prepared with various degrees of titanium doping. One such crystal reveals through X-ray diffraction a lattice parameter change corresponding to a 10% to 15% incorporation of Ti into the ZrGeO₄ lattice. A Raman spectrum of the 10–15% titanium-doped ZrGeO₄ along with that of undoped ZrGeO₄ for comparison is shown in Figure 4. The shifts and broadening of the ZrGeO₄:Ti⁴⁺ Raman bands relative to those in undoped ZrGeO₄ are significant and comparable to those in the spectrum of ZrGeO₄:V⁴⁺ shown in Figure 2. The most significant shifts occur for the bands at (ZrGeO₄ peak positions) 295.3, 378.9, 406.5, and 565.6 cm^-1 to 286.2, 374.1, 401.3, and 559.8 cm^-1 in the ZrGeO₄:Ti⁴⁺ spectrum, respectively. Also, a band emerges at 640.1 cm^-1 with Ti doping that is not present in the spectrum of pure ZrGeO₄. That portion of the spectrum between 150 and 425 cm^-1 has been expanded in Figure 5 so that you can clearly see the significant changes to several of the bands. The Raman bands most affected by Ti doping are shown along with their mode assignments in Table I. Similar to our observations with V doping, we see that the low energy modes at 171.3 and 255.2 cm^-1 (ZrGeO₄ peak positions) are weakly or not affected at all by Ti doping. That only some of the bands shift as a result of Ti doping suggests that Ti is not indiscriminately positioned, but rather preferentially occupies specific lattice sites. The fact that the bands most affected by Ti doping are all assigned to lattice vibrational modes involving GeO₄ motion indicates that the Ge position is the site of occupancy.

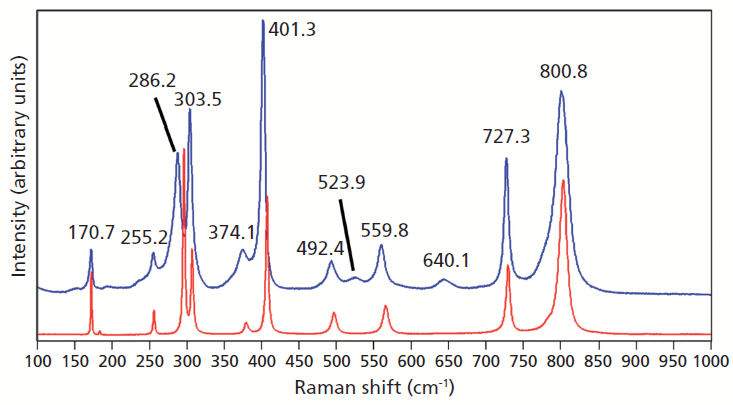
Figure 4: Raman spectra of single crystals of ZrGeO₄ (red) and ZrGeO₄ doped with Ti (blue).

To further characterize the effect of Ti doping on the Raman bands of the host lattice ZrGeO₄, we make use of what I have previously called Ramancrystallography (5). Raman crystallography can be used for the characterization of the atomic structure of solids because Raman scattering depends on the polarization and direction of the incident laser light, the crystal symmetry and orientation of the solid sample, and the direction and polarization of the collected Raman scattered light. The Raman polarizability tensor is fixed relative to the positions of the atoms and the directions of the bonds between them. Therefore, for a crystal fixed in space the Raman signal is dependent on the crystal symmetry and orientation of the sample relative to the direction and polarization of the incident and collected light. The expression for Raman scattering intensity used in the application of Raman crystallography is

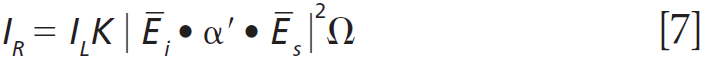
Click here to view full-size graphic

where I_R is the Raman scattering intensity, I_L is the intensity of the incident laser light, K is a factor incorporating the dependence on the frequency of the incident laser light and the standard cross section, E_i the polarization of the incident light, and E_s and Ω are the polarization and solid angle, respectively, at which scattered light is collected. The significance of this expression for work with crystals is that Raman scattering intensity is proportional to the square of the dot product of the incident electric field vector, Raman polarizability tensor, and scattering vector. It is of great importance that the forms (whether elements are zero or nonzero) of the polarizability tensors for crystals are dictated by the symmetry point groups of the crystal class to which the material belongs. The absolute magnitude of the tensor elements is dictated by the specific chemical bonds between the atoms. However, whether a tensor element is zero or nonzero is entirely dictated by the crystal symmetry. The forms of the Raman tensor are the same for all lattice vibrational modes of the same symmetry species. Therefore, the normalized Raman signal strength as a function of crystal orientation should be the same for all Raman bands assigned to vibrational modes of the same symmetry species.

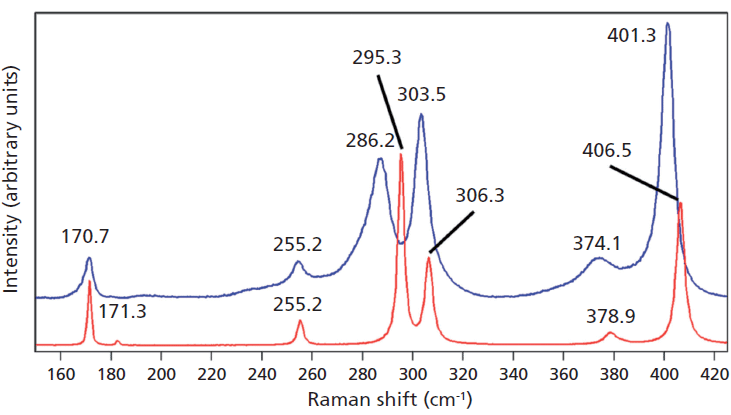
Figure 5: Raman spectra of single crystals of ZrGeO₄ (red) and ZrGeO₄ doped with Ti (blue). Ti occupancy of the Ge site causes Raman bands to shift and broaden relative to those in undoped ZrGeO₄.

The experimental arrangement for Raman crystallography used a 100× microscope objective to focus a 532-nm laser beam incident upon the <001> face of the ZrGeO₄ crystal doped with Ti. Backscattered light was collected in two configurations with the analyzer either parallel or perpendicular with respect to the incident polarization. Spectra were then acquired in 5° rotational increments as the crystal was rotated about the axis normal to the <001> crystal face. The Raman responses from this measurement of two B_g modes at 171 and 727 cm^-1 and with the Raman analyzer oriented perpendicular to the incident laser polarization are shown in Figure 6. The variations of signal strength with crystal orientation are the same for the 171 and 727 cm^-1 bands as we would expect for two bands of the same symmetry species. Note that these two bands are among those that manifest little change in their position or width as a result of Ti doping. However, as you can see in Figure 5, the 401 cm^-1 band in the Ti-doped ZrGeO₄ spectrum is significantly shifted relative to its counterpart in the undoped ZrGeO₄ spectrum. This band too belongs to the B_g symmetry species. The Raman responses from this measurement of two B_g modes at 401 and 727 cm^-1 and with the Raman analyzer oriented perpendicular to the incident laser polarization are shown in Figure 7. Here we have again plotted the response of two bands of the same symmetry species, but the Raman crystallographic responses are no longer in phase. We note that the 401 cm^-1 band has been significantly affected by Ti doping as manifested in its shift to a lower wavenumber. The plots of these two B_g Raman responses as a function of crystal orientation are no longer in phase because of the disruption of the crystal lattice symmetry by the presence of the Ti dopant and its effect on the B_g mode at 401 cm^-1.

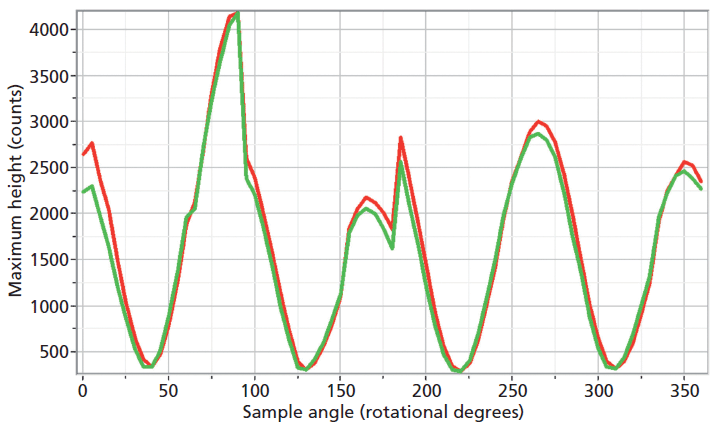
Figure 6: Raman signal strength of 171 cm^-1 (green) and 727 cm^-1 (red) bands of the Ti-doped ZrGeO₄ <001> crystal face as a function of crystal orientation in the <001> plane and with the Raman analyzer oriented perpendicular to the incident laser polarization. Both bands belong to the B_g symmetry species.

Chemical Bonding and the Doping of ZrGeO₄

Here we elaborate on the band structure analysis and offer an explanation for the effects of Ti doping on the Raman spectrum of ZrGeO₄. The affected bands have two common characteristics. Specifically, their Raman tensors have nonzero α_xx and α_xy tensor elements and that they can be assigned to GeO₄ rotation or Ge-O bending motions within the ab-plane. The Γ_lib mode in Table I is a GeO₄ rotation. We assign the Γ_int bands in Table I to Ge-O bending motions based on the application of the site group method to correlate the S₄ site symmetry species to an XY₄ free molecule of T_d symmetry. The correlation diagram for the GeO₄^4- group in the ZrGeO₄ crystal is shown in Figure 8.

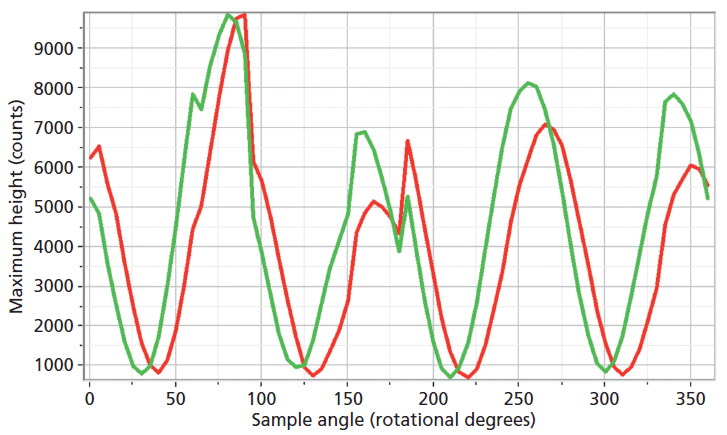
Figure 7: Raman signal strength of 401 cm^-1 (green) and 727 cm^-1 (red) bands of the Ti-doped ZrGeO₄ <001> crystal face as a function of crystal orientation in the <001> plane and with the Raman analyzer oriented perpendicular to the incident laser polarization. Both bands belong to the B_g symmetry species.

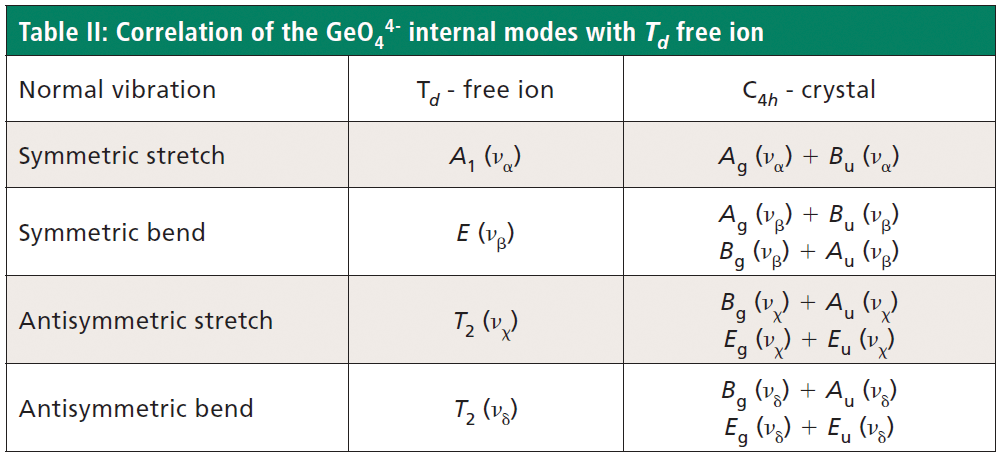
The free GeO₄^4- group with T_d symmetry has four normal vibrational modes consisting of A₁ (υ_α) symmetric stretch, E (υ_β) symmetric bend, T₂ (υ_χ) antisymmetric stretch, and T₂ (υ_δ) antisymmetric bend. The symmetry of the free GeO₄^4- group is lowered to S₄ in the crystal, and the free ion T_d modes can be correlated to the internal modes of the factor group C_4h ZrGeO₄ crystal. That correlation of the Td local vibrational modes to C_4h phonons is shown in Table II.

Regarding our assignment and correlation of ZrGeO₄ bands to local Td modes, we expect the stretching modes to constitute the highest energy phonons in the spectrum, and based on our previous work the bands at 729.4 (B_g), 782 (E_g) (shoulder), and 803.1 cm^-1 (A_g) have the appropriate symmetries to correlate to υ_χ (B_g), υ_χ (E_g) and υ_α (A_g), respectively (1). The remaining Γ_int bands are at 378.9 (A_g), 406.5 (B_g), 496.3 (E_g), and 565.6 cm^-1 (B_g), which by symmetry correlate to υ_β (A_g), υ_β(B_g), υ_δ (E_g) and υ_δ (B_g), respectively. Of those four Γ_int bands, the A_g and B_g modes are among those most affected by Ti doping. Indeed, the bands listed in Table I as those most affected by Ti doping constitute the entire set of combined A_g and B_g bending and rotational modes for ZrGeO₄. There is one E_g bending mode and one E_g rotational mode, both of which are not as strongly affected by Ti doping. Note, however, that the nonzero E_g tensor elements are α_xz, α_zx, α_yz, and α_zy. In contrast, the strongly affected A_g and B_g modes have nonzero α_xx, α_yy, or α_xy (α_yx) tensor elements. Therefore, we conclude that Ti⁴⁺ substitution for Ge⁴⁺ significantly affects Raman bands arising from rotational and bending motions of the GeO₄^4- group about the c-axis, within the ab-plane.

Here we offer an explanation in terms of chemical bonding for the effects of Ti doping on the Raman spectra of ZrGeO₄. The tetrahedral GeO₄^4- group is formed by a combination of the oxygen orbitals and sp³ hybridized atomic orbitals from Ge⁴⁺. However, if Ti⁴⁺ is substituted for Ge⁴⁺, the atomic orbitals of the central atom are no longer sp³ hybridized. The 4s (a₁), 4p (t₂), 3d (e), and 3d (t₂) atomic orbitals of Ti⁴⁺ will, in a tetrahedral coordination, transform to the molecular orbitals a₁, t₂, e, and t₂, respectively. One a₁ and three t₂ molecular orbitals form σ-bonding orbitals in the tetrahedral structure. In particular, note that the t₂ bonding orbitals are formed by a hybridization of Ti⁴⁺ d (t₂) and p (t₂) orbitals. The 3d (e) atomic orbitals would transform to e nonbonding molecular orbitals. However, metal oxides readily form π bonds, and the 3d (e) orbitals can form π-bonding orbitals with the ligand in a tetrahedral structure. If π bonding does occur, then the local electronic structure of the TiO₄^4- tetrahedron is significantly different from that of the sp³ hybridized GeO₄^4- tetrahedron. In particular, we could expect the d_x2_-y2 (e) orbital involved in π bonding to hinder rotation of TiO₄^4- in the ab-plane, thereby damping lattice vibrational modes related to the unhindered rotation of the sp³-hybridized GeO₄^4- tetrahedron. Consequently, Raman bands arising from GeO₄^4- rotations should shift and perhaps broaden to a lower wavenumber, which is what we observe.

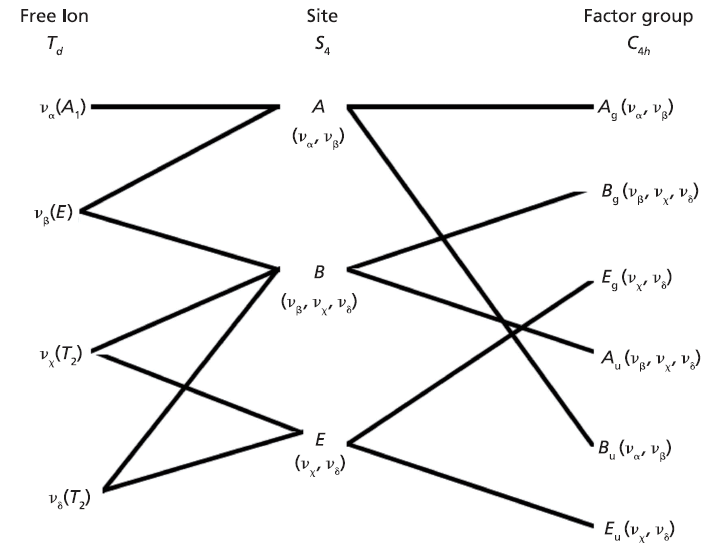
Figure 8: Correlation diagram for the GeO₄^4- group in the ZrGeO₄ crystal.

The explanation and chemical interpretation regarding the chemical bonding of Ti⁴⁺ with surrounding oxygen atoms applies equally well to V⁴⁺ in Ge site occupancy. The transition metal dopants have a far greater effect on the lattice spectrum of ZrGeO₄ than does the lanthanide Tb dopant because of the role their d-orbitals play in chemical bonding to the crystal lattice.

Conclusion

The disruption of crystalline symmetry by dopants or impurities in a crystal can affect the lattice vibrational modes of the host crystal. The manner in which the host-crystal Raman spectrum is affected is related to the site occupancy of the dopant or impurity. Not all bands will be affected equally by the presence of heterogeneity in the crystal. Those Raman bands arising from lattice vibrational modes that involve a significant contribution of atomic motion from the substituted atom will manifest the most significant broadening or shifting of peak position. Raman spectroscopy has been used to characterize the effects of doping ZrGeO₄ with V, Ti, and Tb. We find that whereas all of the modes most affected by Tb, Ti, or V doping are those arising from the GeO₄^4- group, not all of the GeO₄^4- modes are strongly affected by doping. Substitution of either Ti⁴⁺ or V⁴⁺ for Ge⁴⁺ significantly affects Raman bands arising from the rotational and bending motions of the GeO₄^4- group about the c-axis, within the ab-plane. We propose an explanation for the effects by the transition metals based on group and molecular orbital theory.

Acknowledgment

The crystals were prepared by Dr. Pat Lambert of Transparent Materials in Rochester, New York.

References

(1) D.D. Tuschel and P.M. Lambert, Chem. Mater. 9, 2852–2860 (1997).

(2) D. Michel, M.T. Van Den Borre, and A. Ennaciri, Adv. Ceram. 24A (Sci. Technol. Zirconia 3), 555–562 (1988).

(3) M.T. Vandenborre, D. Michel, and A. Ennaciri, Spectrochim. Acta A 45A, 721–727 (1989).

(4) G. Turrell in Practical Raman Spectroscopy, D.J. Gardiner and P.R. Graves, Eds. (Springer-Verlag, Berlin, 1989), chap. 2, pp. 13–54.

(5) D. Tuschel, Spectroscopy 27(3), 22–27 (2012).

David Tuschel

David Tuschel is a Raman applications manager at Horiba Scientific, in Edison, New Jersey, where he works with Fran Adar. David is sharing authorship of this column with Fran. He can be reached at: SpectroscopyEdit@UBM.com