Quantum Cascade Lasers for Infrared Spectroscopy: Theory, State of the Art, and Applications

Miniature, but powerful mid-infrared (IR) quantum cascade lasers (QCLs) have been developed and commercialized recently. Their unique properties make it possible to advance the analytical problem-solving capabilities of IR spectroscopy in many ways. This includes highly sensitive measurements as well as novel applications. Bernhard Lendl of the Institute of Chemical Technologies and Analytics at Vienna University of Technology, Austria, has been researching and developing QCLs for many applications. Spectroscopy recently spoke to Lendl, and to Markus Brandstetter, a member of Lendl's research group, about how QCLs work, the current state of the art, and practical applications of the technology.

Could you summarize the principles of how quantum cascade lasers (QCLs) work, and the state to which they have evolved since their invention in 1994?

BL: Like all lasers, QCLs have to meet three conditions to obtain a stimulated emission and thus light amplification — or in other words, to obtain a gain from a laser:

• Population inversion: a state of the gain medium of the laser, where higher energetic levels are more populated than the lower ones.

• Feedback: the light emission in the gain medium under the first condition is stimulated by photons present in it. Therefore, there must be some portion of emitted photons reinjected into the gain medium.

• Energy supply: a means to maintain the population inversion. In the case of QCLs, like the majority of semiconductor lasers, this is an electrical current.

The main difference between standard semiconductor lasers and QCLs lies in the way population inversion is achieved. Standard semiconductor lasers are designed to have population inversion between the conduction and the valence band. Hence, electrons can undergo transitions between these energetically different levels, causing photon emission (interband transition). Here, the photon energy, and thus the wavelength of the emitted light, is determined by the size of the band gap. Because the band gap itself is more or less determined by the two materials used as gain medium, only a certain emission range is feasible. Unfortunately, the available materials exclude the major part of the mid-infrared (IR) spectral region. In contrast to this conventional approach using bulk semiconductor materials, QCLs are designed to obtain population inversion within the conduction band where transitions can occur (inter-subband transition). This is achieved by using a periodic series of very thin (nanometer-level) layers of different semiconductor materials. By applying an electrical voltage across this structure, a cascade of quantum wells of different size and depth develops. Radiative electron transitions between these wells or subbands can occur, inducing laser emission. The nice thing about this concept is that the energy difference between the subbands can be adjusted by changing the thickness of the thin layers. Hence, layer thicknesses are designed to achieve band-gap sizes that correspond to mid-IR radiation. This is also known as band-gap engineering. Using different designs, narrow- or broad-band media can be designed and produced, mainly using a technique called molecular beam epitaxy.

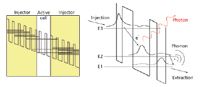
Figure 1: A cascade of quantum wells within the conduction band is the basis for mid-IR laser emission of quantum cascade lasers.

A scheme of a QCL is shown in Figure 1. The gain medium of the laser is realized as a cascade of active cell and injector pairs. The electrons are injected (by means of the electrical current) into the energetic level E3. The system is inverted: The higher level (E3) is more populated than the lower level (E2). In a favorable case, the electrons undergo a radiative transition from E3 to E2. The wavelength of the photon is determined by the energetic spacing between these two levels. The subsequent transition (from E2 to E1) is tailored to be in resonance and thus is very fast and efficient. It serves for extraction of the electrons from level E2 and thus creates conditions for population inversion between levels E3 and E2. After that, the electrons are evacuated by the injector of the following period. By passing a series of such injection–extraction patterns a single electron can cause multiphoton emission.

QCLs are available in Fabry–Pérot (FP), distributed feedback (DFB), and external-cavity (EC) configurations. FP–type QCLs basically consist of the bare QCL chip and show multimode emission at all wavenumbers that meet the Fabry–Pérot condition within the spectral range supported by the QCL's gain curve. DFB QCLs typically have a Bragg grating on top of the QCL chip supporting only a specific emission wavelength. In that way, single-mode emission is achieved and spectral tuning is limited to a few wavenumbers only, which can be realized by changing the operating temperature of the laser chip. Broadband tuning can be achieved by creating an external cavity, which requires placement of a diffraction grating on one end of the laser output (Figure 2). By changing the grating angle, the resonance conditions change and different modes are amplified, leading to spectral tuning of the laser.

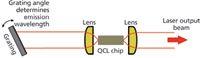
Figure 2: Scheme of a possible EC configuration (Littrow) used for broadband tuning of QCLs.

In theory, every emission wavenumber can be fabricated by proper design of the quantum well structure. Today's situation is that commercially available EC QCLs cover the 4–12 µm range. In practice, however, some wavenumbers are easier to fabricate than others. It can therefore occur that QCLs for specific applications, such as for certain gas absorption lines, occasionally are not commercially available. In addition to room-temperature-operated QCLs in the mid-IR range, liquid-nitrogen-cooled QCLs are available for the terahertz spectral region.

What are the key advantages and limitations of QCLs, and of external-cavity QCLs in particular?

BL: Perhaps the key advantage of QCLs, as opposed to other mid-IR lasers, such as lead salt lasers, is that QCLs can be operated at room temperature. This was already shown two years after their first realization in 1994 for pulsed operation. The first demonstration of room temperature continuous wave (CW) operation was achieved somewhat later, in 2002. Nowadays, almost every QCL chip in the mid-IR can be operated at room temperature so that no liquid nitrogen is required. Some additional key advantages that every QCL offers, regardless of its actual configuration, can be summarized as follows:

• High spectral power density: The optical power density of today's QCLs is in the range of 1 W/cm^-1 for pulsed-mode operation and therefore approximately five magnitudes higher than for a thermal emitter (globar) used in Fourier transform–infrared (FT-IR) spectrometers. Figure 3 illustrates this situation. A high spectral power density is of particular interest for liquid-phase applications where one often has a strong background absorber, such as water. But gas-phase measurements also benefit from the QCL's high optical power density. In quartz-enhanced photoacoustic spectroscopy, for example, the measured signal is directly proportional to the source intensity.

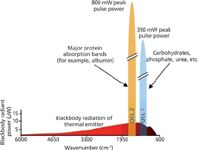
Figure 3: Comparison of the blackbody power typical for the thermal emitters used in FT-IR spectrometers (measured in a Bruker Vertex 80v FT-IR spectrometer) with two EC QCLs currently used by the Lendl group.

• Single-mode emission: Single-mode emission is equivalent to narrow spectral emission lines, which is the prerequisite for highly selective gas-phase measurements. With single-mode DFB-QCLs it is possible to pick out a single analyte-specific rotational-vibrational absorption line that does not interfere with any of the other gases present in the sample. That is why most applications of QCLs in analytical chemistry deal with highly sensitive gas measurements.

• Miniaturization, integration, and wall plug efficiency: QCLs are semiconductor devices and thus they offer high potential for miniaturization and integration. Many efforts are currently being made to integrate the laser, sample unit, and detector in one piece. The resulting sensors systems will offer huge potential in terms of stability and robustness for field applications. Furthermore, miniaturization will assist the work done to increase the wall plug efficiency of QCL-based devices.

In addition, QCLs in the EC configuration offer another important feature: broad tunability and extended possibility for beam modulation.

Concerning the limitations of today's QCLs, the spectral quality and beam quality are parameters that offer room for improvement. Still, a compromise has to be found between maximum tunability (EC configuration) and optimum beam quality (single-mode emission configuration). For a proper spectroscopic application the realization of the best possible optical stability always was and presumably always will be the key challenge. EC QCL devices are particularly challenging in this regard as they include at least one mechanical part — the movable grating. The use of a highly stable microelectromechanical system (MEMS) is one possible path toward fully integrated, and thus more stable lasers. Alternatively, arrays of several DFB-QCLs, which compared to EC QCLs hold the advantage that they do not require any moving parts, can be fabricated and used for applications requiring an extended spectral range. Complementary, sophisticated configurations, such as arrays of ring-cavity surface emitting QCLs as well as multisegment DFB-QCLs, have been shown. Again, these configurations do not require moving parts, while providing a spectral coverage of several tens of wavenumbers.

What is the tunability range of external-cavity QCLs?

BL: The tunability achievable per single EC QCL typically depends on its performance characteristics. In the case of CW-operated mode-hop free EC QCLs, up to several tens of wavenumbers are feasible. Pulsed EC QCLs based on a single chip cover a spectral range of about 200–350 cm^-1. Special chips that contain different gain media can provide a tuning range of up to 600 wavenumbers, or even more. To cover as much as possible of the relevant mid-IR spectral region using a single EC QCL unit, up to three different EC QCLs have been combined internally and placed in one housing.

How does temperature affect the tuning of external-cavity QCLs?

BL: The influence of ambient temperature on the EC QCL can be neglected as long as the maximum operating temperature is not exceeded. EC QCLs operated in CW mode will stabilize at a certain operating temperature and stable tuning is maintained. By changing the temperature of the QCL chip mount, the emission temperature can be fine tuned with a temperature gradient of about 0.3 cm^-1/K. The tuning characteristics of the external grating should, however, not be influenced by the chip's temperature. For pulsed-mode lasers, the situation is different. During the pulses the QCL chip will heat up until an equilibrium temperature is reached. The typical pulse lengths are below 1 µs, which is too short to reach full equilibrium. Because of this heating process, the refractive index of the laser material changes. This results in a shift of the QCL emission mode (laser chirp) toward lower wavenumbers or a higher wavelength, respectively. In contrast to single-wavelength QCLs in distributed-feedback configuration, the QCL chip in an EC configuration is realized as a Fabry–Pérot type. Hence, multiple emission modes, all affected by the temperature shift, will appear. What the user of an EC QCL will actually see at the EC QCL's output aperture will be a small spectral section of this multimode line pattern. More exactly, this will be a section that is determined by the external diffraction grating's position. Figure 4 shows a typical EC QCL output signal measured by time-resolved step-scan FT-IR spectroscopy.

Figure 4: Step-scan time-resolved FT-IR measurement of an EC QCL (Daylight Solutions, Inc.) with a 0.1-cm-1 spectral resolution and 2-ns time resolution, and a laser pulse length of 500 ns.

One area where you have made use of QCLs is in the development of a mid-IR absorption sensor for routine point-of-care blood analysis, for use in an intensive care environment. What analytes can be effectively measured with this technique, and at what levels?

MB: In principle, all IR-active analytes in blood, above a certain concentration level, can be measured. Consequently, some blood ions, such as K⁺ or Na⁺, cannot be accessed directly by this approach. Currently, we are able to quantify glucose, lactate, triglycerides, total cholesterol, albumin, total protein, urea, and fibrinogen in a single measurement. This was proven for blood sera from regular blood donors as well as in a clinical setting with blood plasma samples from critically ill patients. The achievable detection limits are different for each analyte, but for most analytes they are within the required range for clinical application. Linearity, an important aspect in this field of application, was maintained for the whole physiological range as well as for pathological concentrations.

What were the challenges involved in this application?

MB: For this specific application we chose an EC QCL from Daylight Solutions that offered the maximum tuning range available (200 cm^-1) on the market at the time we purchased the laser (2009). This was necessary to cope with the overlapping bands typical for liquids containing multiple analytes. The first big challenge was then to thoroughly characterize this new mid-IR light source. During this time we learned a lot about the strengths and weaknesses of this technology. Because we wanted to perform multianalyte detection from the beginning, one challenge was to keep the noise level as low as possible to facilitate proper multivariate data analysis. Here, the experience gained during comprehensive laser characterization using time-resolved FT-IR spectroscopy was essential.

For this application, what method would QCLs be replacing?

MB: Nowadays, point-of-care analyzers for clinical chemistry rely almost exclusively on enzyme based assays, and for each blood constituent of interest, a suitable assay is employed. The QCL point-of-care blood sensor benefits from the advantages of mid-IR spectroscopy: All parameters are determined simultaneously and directly without the use of reagents. Because no reagents are required, there is also no consumption of sample during measurement. Therefore, if an appropriate interface can be developed, this technology would be suitable for continuous monitoring of patients in intensive care units. An analyzer based on an EC QCL would, as of today, require a higher initial investment compared to standard blood gas analyzers. However, given the reagent-free measurement approach, operational costs would be much lower.

Is this technique now robust enough for routine clinical use?

MB: Robustness of the optical setup, including the EC QCL and the mid-IR detector, was already achieved at an early stage of sensor development. However, what we learned from people working in the field of clinical analysis was that the sample interface — in our case, the flow-through transmission cell — determines the analyzer's robustness, and requires a minimum optical path of 100 µm. The water background in blood does absorb the major fraction of the incident radiation, which implies short interaction lengths (<50 µm in the carbohydrate region around 1100 cm^-1) when using weak thermal emitters. This is one of the reasons why conventional mid-IR spectroscopy has not made it into the clinical laboratory so far. QCLs now make it possible to use transmission cells with pathlengths larger than 160 µm. This was the key feature to make the technique robust enough for clinical use — besides the obvious prerequisite of room-temperature operation.

You have also applied QCLs with mid-IR spectroscopy as a real-time analyzer for monitoring the degree of contamination of cleaning water in a clean-in-place (CIP) system for a biopharmaceutical manufacturing environment. What results have you seen with this application?

BL: Here, we applied an adapted version of the above mentioned blood sensor for real-time contamination monitoring during the cleaning process of industrial reactors used in the biopharmaceutical industry. The idea is to have real-time information on the actual contamination level during the cleaning process. This can facilitate process optimization in pharmaceutical engineering, which would not be possible with state-of-the art total organic carbon (TOC) analyzers that are working on a much longer time scale. During our studies we observed that in some cases the cleaning process was already finished when the first result of the TOC device was ready. At the same time the QCL sensor was able to measure more than 1000 data points. The achieved detection limits were in the low parts-per-million region. Of course, there is still room for improvement, particularly regarding the spectral performance of the EC configuration, which is currently limiting the achievable signal-to-noise levels.

A third area where you have applied QCLs is measuring petroleum hydrocarbons in water. Could you outline that setup?

BL: There is a need to measure the residual oil content in production and wastewater, such as in the oil-producing industry. In fact, this is an old analytical problem that had been solved in the past by a simple IR spectroscopic method. This old but very popular method was based on a liquid–liquid extraction step using Freon 113, an organic solvent that does not contain any C-H bonds. Therefore, it was possible to quantify the amount of extracted oil by measuring the C-H stretch absorption around 3000 cm^-1 using a simple IR spectrometer. This old method was fast, highly precise, simple to use, and available in a portable format. However, because chlorofluorocarbons (CFCs) and Freon 113 in particular are responsible for destroying the protective ozone layer in the stratosphere, this analytical method was banned at least in the industrial world by the Montreal protocol. Since then, no satisfactory replacement method has been developed that is both environmentally friendly and of similar simplicity and metrological quality. In this respect, the advent of QCLs radically changed the situation. Now, for the first time, it is possible to determine petroleum hydrocarbons in water by performing a liquid–liquid extraction using the environmentally friendly solvent cyclohexane and subsequent IR spectroscopic measurement of the extracted oil. This is possible because the small spectral differences between the cyclic solvent and petroleum hydrocarbons are sufficient when a QCL is used for measurement. In 2011, an ASTM test method (ASTM 7678-11) was released based on this measurement principle, and an instrument meeting the requirements of this test method was developed by our spin-off company QuantaRed Technologies. This instrument is now available worldwide through Eralytics.

Why did you choose this application?

BL: We selected this application because there was a clear need for a portable, rapid, reliable, and environmentally friendly method for measuring oil in water. The old and established technology based on Freon 113 could no longer be used because of regulatory reasons. Other alternative methods based on gas chromatography, gravimetry, or fluorescence did not meet the needs in terms of speed, selectivity, portability, and robustness. In addition, these customers can accept the price range of a QCL-based analyzer.

What results have you achieved?

BL: Most importantly, our costumers are happy with the performance of this analyzer, which works fine not only in an analytical laboratory but also at demanding locations such as oil rigs. As of today, this QCL-based analyzer is in operation in four continents and in more than 14 countries. Through the success of this product we also have been able to demonstrate that QCL technology is now mature enough to allow the use of these lasers for routine use in chemical analyzers. Hopefully, this success will help to motivate other researchers or companies to develop novel QCL-based solutions for old or new problems in analytical chemistry.

You have noted that QCLs can be used for detection in liquid chromatography for both qualitative and quantitative analysis. What advantages would a QCL-based detector have over other chromatography detection systems such as UV–vis diode-array detection?

BL: Clearly, the advantage lies in the direct molecular specific information available in the mid-IR range as opposed to the UV–vis spectral range and in its nondestructive character as opposed to mass spectrometry. Therefore, a QCL-based detector may be added to any separation system, including liquid chromatography as well as capillary electrophoresis. As the available spectral coverage by one laser system (such as an EC QCL) is increasing, QCLs are becoming a more generally applicable option that can be used in addition to, or even as a replacement of traditional detectors. Even if only 0.1% of the worldwide separation systems would use a QCL detector the market would be huge. Recently, using FT-IR detection in capillary liquid chromatography, we could demonstrate that thanks to modern multivariate data analysis techniques, direct IR detection in a flow cell is even compatible with gradient techniques. Therefore, I am optimistic that we will see QCL-based detectors as an additional option for different applications in separation sciences in the near future.

What should we expect to see from QCLs in the next 5–10 years? Is there real potential for QCLs to develop into a viable alternative for FT-IR spectrometers?

BL: This is a good question. First of all, we will witness a further improvement in basic QCL technology in terms of spectral coverage, output power, wavelength stability, and CW operation. However, I do not expect QCL technology to replace the established FT-IR spectrometers. FT-IR technology also has evolved in recent years, and today, in addition to high-end research FT-IR spectrometers, surprisingly well performing, cost effective, and portable FT-IR instruments are available as well. So, I think it will be difficult to replace these instruments. However, instead of replacing standard FT-IR spectrometers, which all use a thermal light source emitting noncoherent light, I believe that QCL technology will enable the development of novel measurement techniques and applications that cannot be performed using FT-IR technology based on thermal light sources. These new techniques and applications will make use of the particular characteristics of QCLs, which I see in their high spectral power densities and miniature size, as well as the fact that QCLs do emit polarized radiation. Furthermore, QCLs can be operated in CW as well as pulsed mode with high repetition rates. Therefore, QCLs seem to be well suited for use in stand-off detection systems, for photoacoustic detection as well as in vibrational circular dichroism spectroscopy. In addition, fully integrated sensor devices for dedicated applications can be envisioned, too.

What are your next steps in your work on QCLs?

BL: In my research group at the Vienna University of Technology and in cooperation with QuantaRed Technologies, we plan to continue the development of QCL-based analyzers and sensors for the liquid phase. This will include lab-on-a-chip based systems for time-resolved analysis of chemical reactions in solution as well as integrated sensor systems for dedicated applications. As a complementary focus, we recently started activities in gas sensing where we use open-path measurement strategies, photoacoustic detection, and absorption measurements in a multireflection cell. Here we also aim to develop lightweight, portable sensor systems for applications in environmental and process analytical chemistry. A few months ago we started work in the area of near-field mid-IR imaging. We are building a system that will combine atomic force microscopy and EC QCLs. In my laboratory, this work is still in its infancy; however, we are happy that we can learn from our international colleagues and friends who already have demonstrated that this combination is indeed feasible.

Markus Brandstetter is a graduate student in the research group of Bernhard Lendl. In his PhD thesis, he developed the application of EC QCLs for blood analysis.

Markus Brandstetter

Bernhard Lendl is a professor of analytical chemistry at the Institute of Chemical Technologies and Analytics at Vienna University of Technology, Austria. Direct correspondence to: bernhard.lendl@tuwien.ac.at

Bernhard Lendl